Plotting Longitudinal Data in R




Introduction
For the presentation purposes of this post, simulated data were produced from already existing data of SARSSURV study.
library(ggplot2)
library(ggradar)
library(ggpubr)
library(dplyr)
library(tidyr)
library(faux)
data=sim_df(raw_data, 2000)
BoxPlots
Boxplots are a valuable tool for presenting longitudinal data, allowing for effective visualization of changes over time and comparisons between groups. The graphical representation makes it easy to highlight trends over different time periods and showcase distinctions between various groups.
Bellow there is a sample code to produce such boxplots:
bxp <- ggboxplot(data, x = "vax_brand", y = "logigg",
color = "vax_brand", palette = "jco",
#add = "jitter",
facet.by = "measur",
short.panel.labs = T
)+
labs(x = "Vaccines", y = "Log scale Anti-spike IgG (BAU/ml)")+ labs(color = "Vaccines")
bxp
library(rstatix)
stat.test <- data %>%
group_by(measur) %>%
t_test(logigg ~ vax_brand) %>%
adjust_pvalue(method = "bonferroni") %>%
add_significance("p.adj")
stat.test
# Additional statistical test
# Add p-values of `stat.test` and `stat.test2`
# 1. Add stat.test
stat.test <- stat.test %>%
add_xy_position(x = "vax_brand", dodge = 0.8)
bxp.complex <- bxp + stat_pvalue_manual(
stat.test, label = "p.adj.signif", tip.length = 0.03,step.increase = 0.1
)
significant_stat.test <- stat.test %>%
filter(p.adj < 0.05) # Adjust the significance level if needed
# Plot only the significant comparisons
bxp.complex <- bxp +
stat_pvalue_manual(
significant_stat.test,color="black", label = "p.adj.signif", tip.length = 0.02
) +
theme_bw()
Scatter plot
One of the initial steps is to visualize the repeated measurements over time and graphically test for linear or non-linear trends. Such graphs play a crucial role in guiding you towards a modeling strategy afterward.
Sample code bellow:
p<-ggplot(data, aes(x=timePoints, y=covidIgG,group=vax_brand,color=vax_brand)) +
geom_point(size = 1)+
xlab("Days since booster Vaccination")+
ylab("Anti-spike IgG (BAU/ml)")+
ggtitle("")+theme_classic(base_size = 12)+
geom_smooth(se = T, method = "lm")+ theme(legend.position="bottom")+
labs(color="Booster")+ scale_color_lancet()
p=p+ theme(axis.text.x = element_text(angle = 0, vjust = 0.5, hjust=1))+ theme(legend.text = element_text(size = 8))
p=p+scale_y_continuous(breaks = scales::pretty_breaks(n = 6))
p=p +
theme(plot.background = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank() )+
theme(panel.border= element_blank())+
theme(axis.line.x = element_line(color="gray33", size = 0.7),
axis.title.y = element_text(size = 12),
axis.text.y = element_text(size = 12,color="gray33"),
axis.text.x = element_text(size = 12,color="gray33"),
axis.title.x = element_text(size = 12),
axis.line.y = element_line(color="gray33", size = 0.7),
strip.text.x = element_text(size=rel(2.5)))+
theme(text=element_text( family="Arial"))

Radar Plot
A compelling method for visualizing multiple variables concurrently in a plot while minimizing noise is the radar plot. This type of plot effectively communicates both the absolute values and the temporal changes to the reader. It provides a clear representation of the magnitude of true values and their fluctuations over time.
Sample code for the radar plot bellow:
ggradar(data,
grid.max = 75,
base.size = 6,
font.radar = "sans",
values.radar = c("0%", "35%", "75%"),
axis.labels = colnames(result)[-1],
grid.min = 0,
grid.mid = 35,
grid.line.width = 0.5,
plot.extent.x.sf=1.5,
plot.extent.y.sf=1.5,
gridline.min.colour = "grey",
gridline.mid.colour = "#007A87",
gridline.max.colour = "grey",
grid.label.size = 4,
axis.label.offset = 1.15,
axis.label.size = 4,
axis.line.colour = "grey",
group.line.width = .7,
group.point.size = 1,
background.circle.transparency = 0.4,
background.circle.colour = "#5CB85C",
group.colours = lcols,
legend.title = "Prevalence",
legend.position = "bottom",
plot.title = "",
legend.text.size = 12,
fill = T,
fill.alpha = 0.2,
label.centre.y = 0,
gridline.min.linetype = "longdash",
gridline.mid.linetype = "longdash",
gridline.max.linetype = "longdash"
)
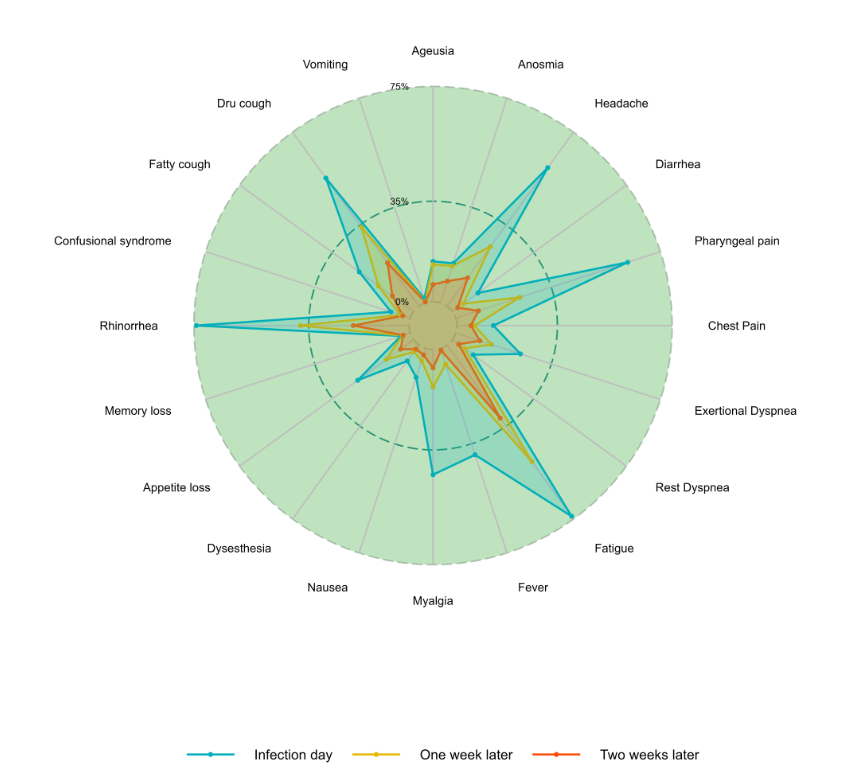
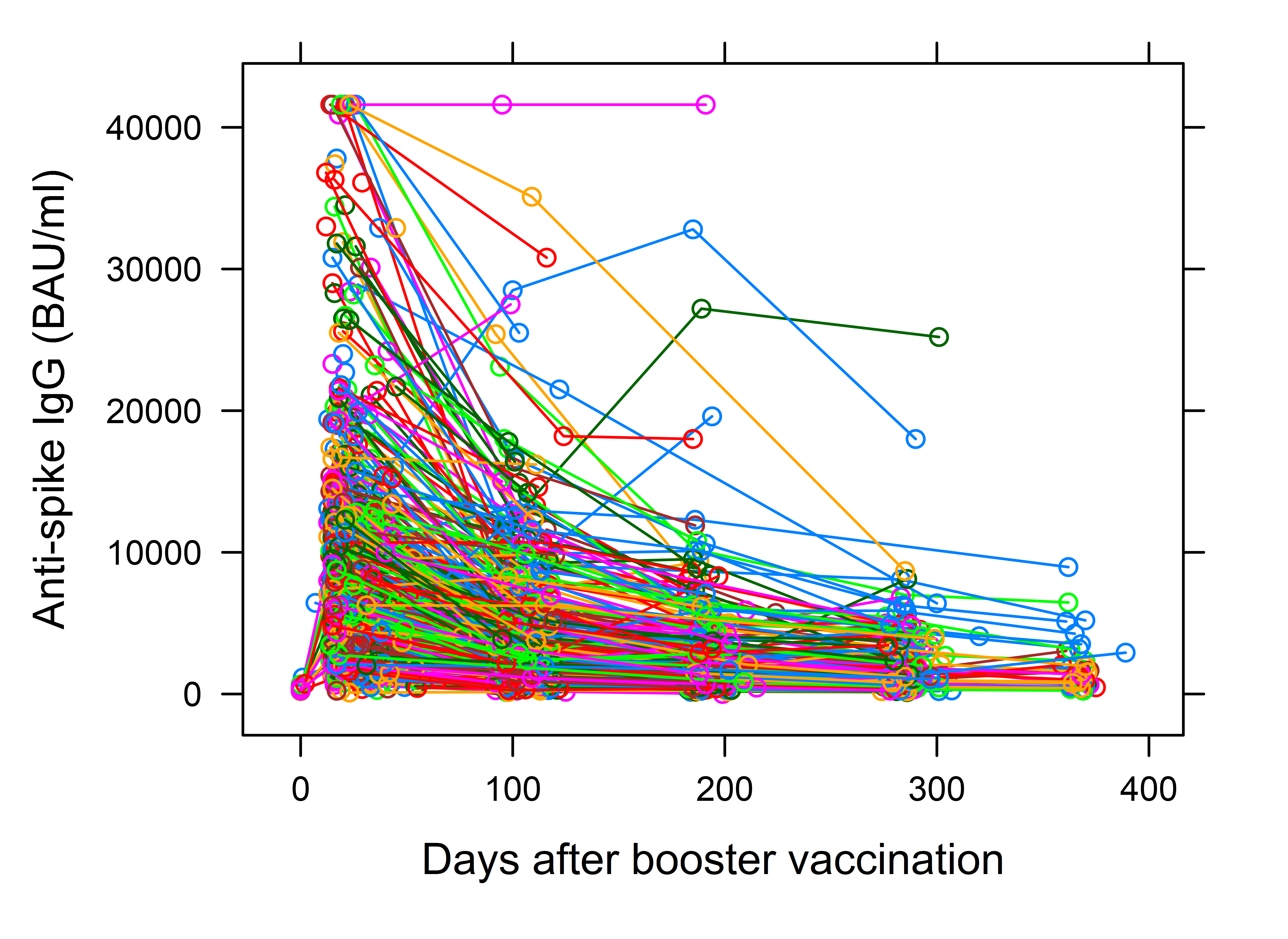
Spaghetti Plot
A lot of times, in the process of longitudinal data modeling, linear mixed models (LME) are applied. Linear mixed models make use of random effects. A first visual idea before moving to a modeling technique is to create a spaghetti plot and graphically check the differences in baseline measurements and the individual temporal trends.
Sample code for a spaghetti plot bellow:
xyplot(IgG ~ boost$time , data = data, groups = IdParticipant,
type = "b", xlab = "Days after booster vaccination", ylab = "Anti-spike IgG (BAU/ml)",
main = "")
Enjoy Reading This Article?
Here are some more articles you might like to read next: